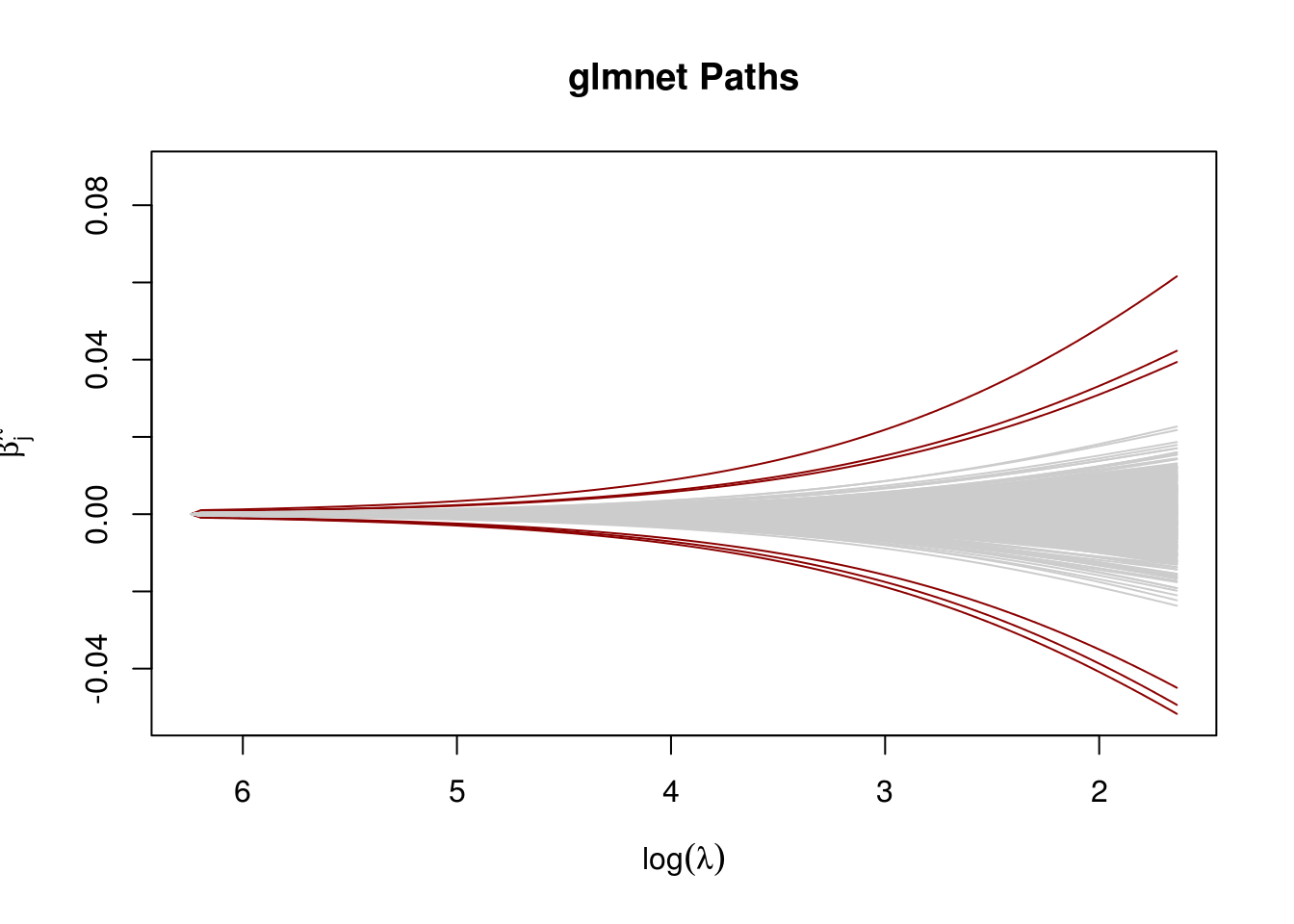
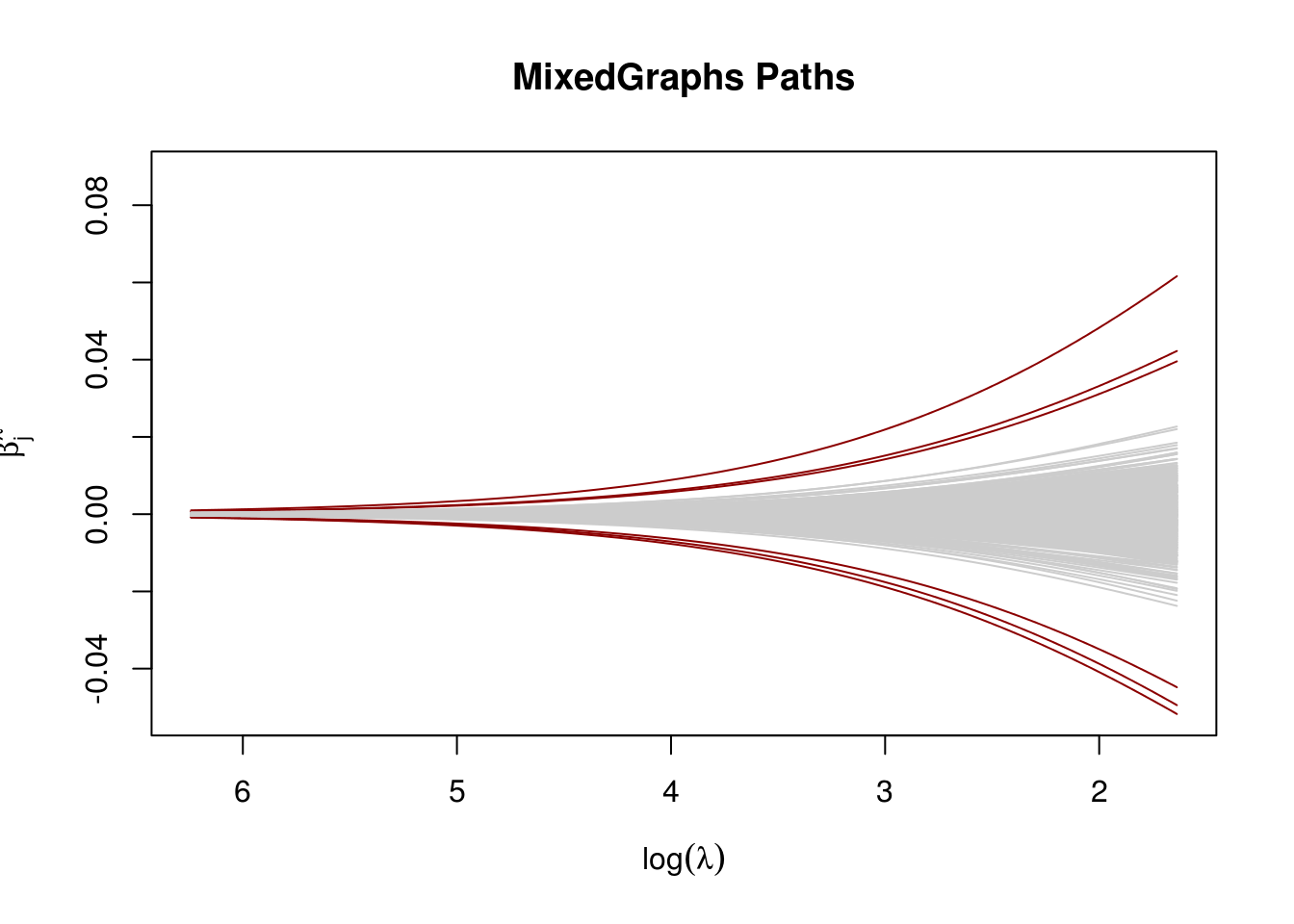
Newton with ridge
Ridge regression
The MixedGraphs package support three different types of data, “gaussion”, “logistic” and “poisson”.
Gaussian
\begin{align} f(\mathbf{\beta}) &= \frac{1}{2n} {\| \mathbf{y} - \mathbf{o} - \mathbf{X} \mathbf{\beta} \|}_2^2+ \frac{1}{2}\epsilon\| \mathbf{\beta} \|_2^2 \\ \mathbf{\beta}^{(k)} &= (\mathbf{X}^T \mathbf{X} / n + \epsilon\mathbf{I})^{-1} \mathbf{X}^T(\mathbf{y} - \mathbf{o})/n \end{align}Logistic
\begin{align} f(\mathbf{\beta}) &= \frac{1}{n} \sum_{i=1}^{n} [\log (1 + e ^ {o_i + \mathbf{x_i} \mathbf{\beta}}) - y_i(o_i + \mathbf{x_i} \mathbf{\beta})] + \frac{1}{2}\epsilon\| \mathbf{\beta} \|_2^2 \\ \nabla_\beta(f) &= \big(\frac{1}{n} \sum_{i = 1}^{n} \frac{x_{ij}}{1 + e ^ {- ({o_i + \mathbf{x_i}\mathbf{\beta}})}} - y_{i} x_{ij} \big)_j + \epsilon \mathbf{\beta} \\ \mathcal{H}_\beta(f) &= \big(\frac{1}{n} \sum_{i = 1}^{n} \frac{x_{ij}x_{jk}e ^ {- ({o_i + \mathbf{x_i}\mathbf{\beta}})} }{{(1 + e ^ {- ({o_i + \mathbf{x_i}\mathbf{\beta}})})}^2}\big)_{jk} + \epsilon\mathbf{I}_{p\times p} \end{align}Poisson
\begin{align} f(\mathbf{\beta}) &= \frac{1}{n} \sum_{i=1}^{n} [- y_i(o_i + \mathbf{x_i} \mathbf{\beta}) + e ^ {o_i + \mathbf{x_i} \mathbf{\beta}} ] + \frac{1}{2}\epsilon\| \mathbf{\beta} \|_2^2 \\ \nabla_\beta(f) &= \big( \frac{1}{n} \sum_{i=1}^{n} - y_ix_{ij} + x_{ij} e ^ {o_i + \mathbf{x_i} \mathbf{\beta}}\big)_j + \epsilon \mathbf{\beta}\\ \mathcal{H}_\beta(f) &= \frac{1}{n}(x_{ij}x_{jk}e^{o_i + \mathbf{x_i}\mathbf{\beta}})_{jk} + \epsilon\mathbf{I}_{p\times p} \end{align}Compare with glmnet
library("glmnet")
library("MixedGraphs")
n <- 200; p <- 500
s <- 6; ## True sparsity
set.seed(8)
X <- matrix(rnorm(n * p), ncol=p)
beta <- rep(0, p);
beta[1:s] <- runif(s, 4, 6) * c(-1, 1)
y <- X %*% beta + rnorm(n)
y <- y / sd(y)
glmnet_fit <- glmnet(X , y, alpha = 0, standardize=FALSE)
glmRidge_fit <- glmRidge(X, y, lambda = glmnet_fit$lambda, thresh = 1)